近期，力学所非线性力学国家重点实验室的研究团队综合运用基于N-S方程的数值模拟、Floquet 全局稳定性分析、动力学模态分解（DMD）三种不同方法，揭示了无来流条件下反相对摆翼的尾迹发生对称破缺的物理机理。以上成果以 “ Instability mechanisms of symmetry breaking in the wakes of two anti-phase pitching foils at zero free-stream velocity” 为题发表在Physics of Fluids上。

通过求解N-S方程的模拟，他们观察到由“间距比”和“雷诺数”组成的二维参数空间存在尾迹稳定性特征不同的6个区域（如图2所示）。 在较低雷诺数下，尾迹总能保持对称性。当超过某个临界雷诺数时，尾迹就会发生对称破缺。这个临界雷诺数的大小与两翼间距有关。在不同的间距和雷诺数条件下，不稳定尾迹的演化可能分别呈现以下5种行为：（1）二次涡街重组；（2）涡对并后的二次涡街重组；（3）尾迹倾斜；（4）尾迹失稳后恢复对称性；（5）出现双股的同相摆动涡街。

通过Floquet全局稳定性分析，他们发现对称破缺发生的根源在于一个反对称Floquet模态失稳（如图3所示）。Floquet稳定性分析的结果能够很好地预测图2中的临界稳定中性线位置以及不同的尾迹失稳类型。他们还进一步采用动力学模态分解（DMD）方法，分析了求解N-S方程得到的对称破缺初步阶段的流场数据。DMD分析指出的对称破缺机理与Floquet稳定性分析的结果完全一致。

力学所博士研究生张治愚为本文的第一作者，张星研究员为通讯作者。该研究工作得到国家自然科学基金项目和中国科学院战略性先导科技专项的支持。

论文链接：https://doi.org/10.1063/5.0196194

图1 物理模型示意图

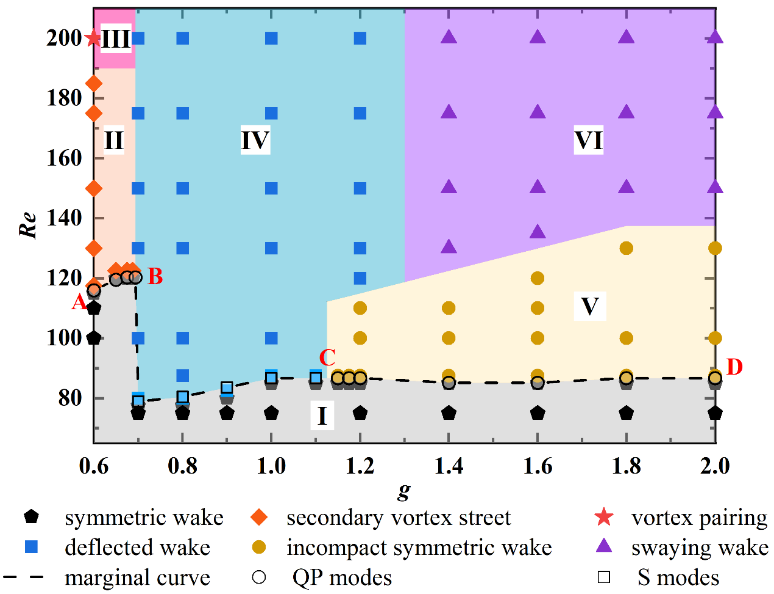
图2参数空间（g, Re）上的尾迹类型分布I：稳定对称尾迹；II：二次涡街；III：涡对并后二次涡街；IV：倾斜涡街；V：对称性可恢复尾迹；VI：双股同相摆动涡街

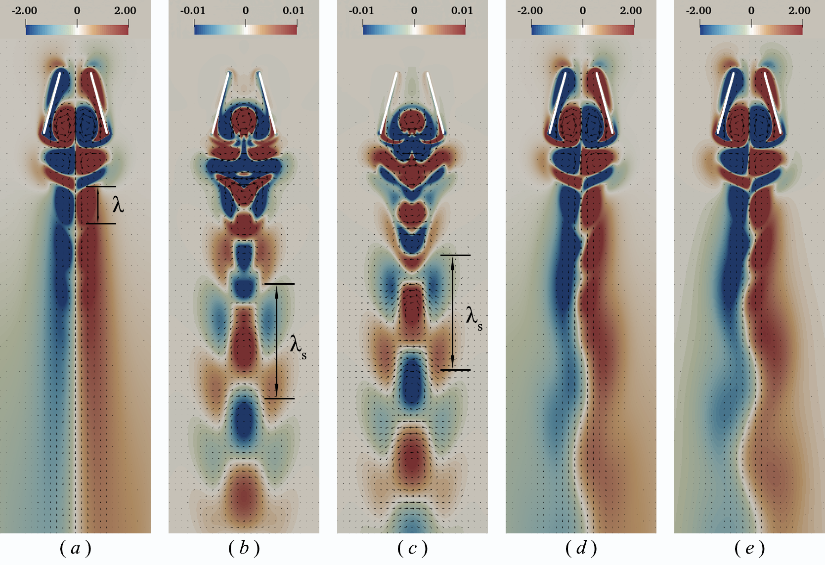
图3 不稳定区域II区算例的涡量图（a）基本流；（b，c）不稳定Floquet模态的实部与虚部；（d）基本流与Floquet模态的叠加；（e）求解N-S方程的结果